Breakpoint regression in Stan

Two lines diverged at a particular point.

UdeS
stan
QCBS
Author

Andrew MacDonald

Published

August 5, 2023

library(ggplot2)
library(tidyverse)
library(tidybayes)
library(cmdstanr)

Two (or more) relationships

In breakpoint regression, we think that the relationship between two things can be described by two lines which alternate at a specific point.

When might this happen? One case is when a rate is determined by the minimum value of two functions1. For an example, consider cars driving down a series of roads. The roads vary in their speed limit, and each car is driven by very lawful drivers who always drive precisely the speed limit

tibble(x = 0:1, y = 0:1) |> 
  ggplot(aes(x = x, y = y)) + 
  geom_abline(slope = 1, intercept = 0) + 
  labs(x = "speed limit", y = "Car speed")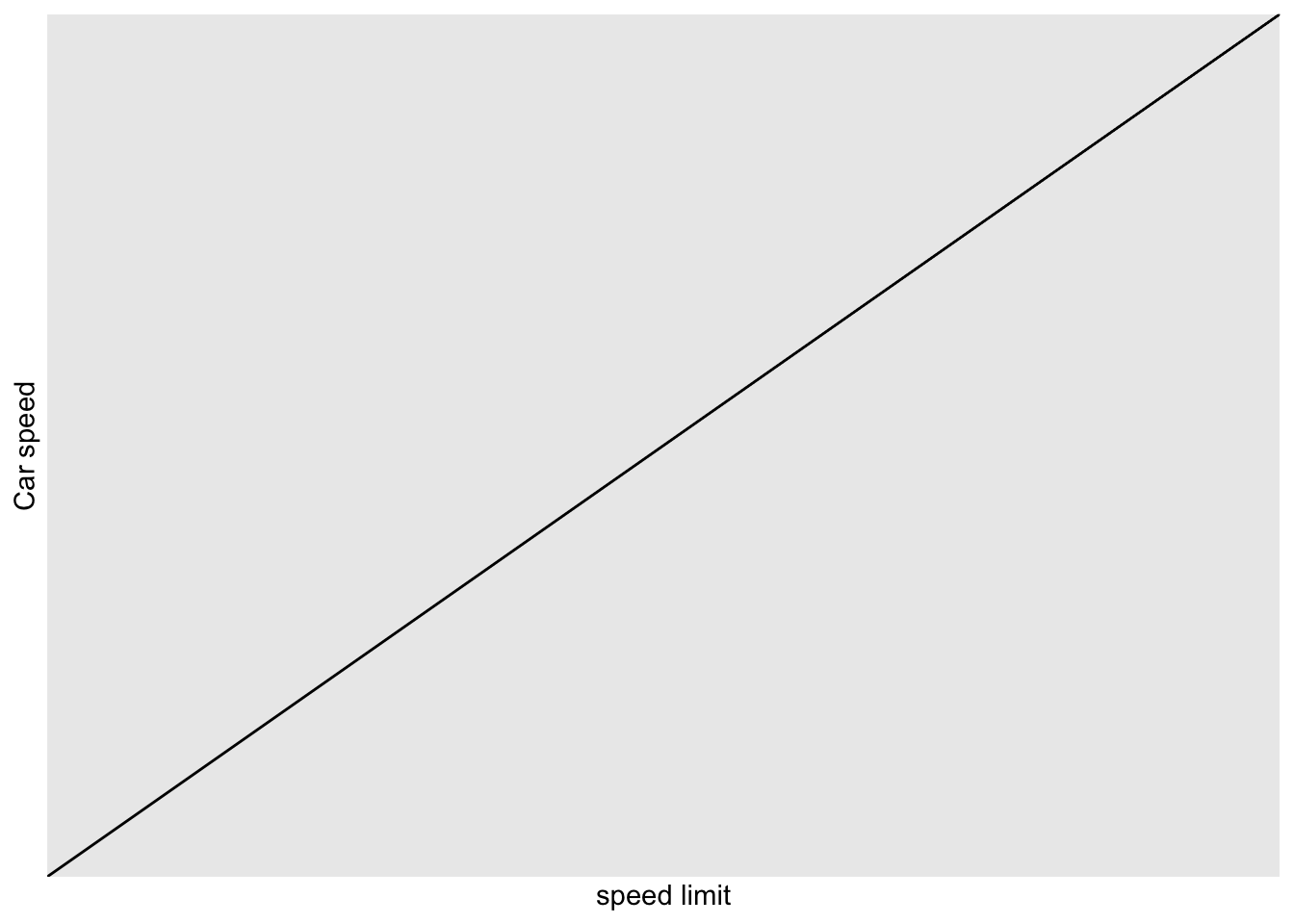

However, some of these highways have VERY high speed limits. The cars, however, can’t keep up: eventually they hit their max speed. When that happens, the lawful drivers hold steady at the fastest speed their car can maintain. Together, you get a kind of “hockey stick” shape:

tribble(~ limit, ~ max,
        0, 0,
        200, 200) |> 
  ggplot(aes(x = limit, y = max)) + 
  geom_point(col = "white") + 
  geom_abline(slope = 0, intercept = 100, lty = 2, lwd = 2, col = "grey") + 
  geom_label(aes(x = 10, y = 105, label = "Max speed")) + 
  geom_abline(slope = 1, intercept = 0, lty = 2, lwd = 2) + 
  theme_classic() + 
  labs(x = "Speed limit", y = "Car speed")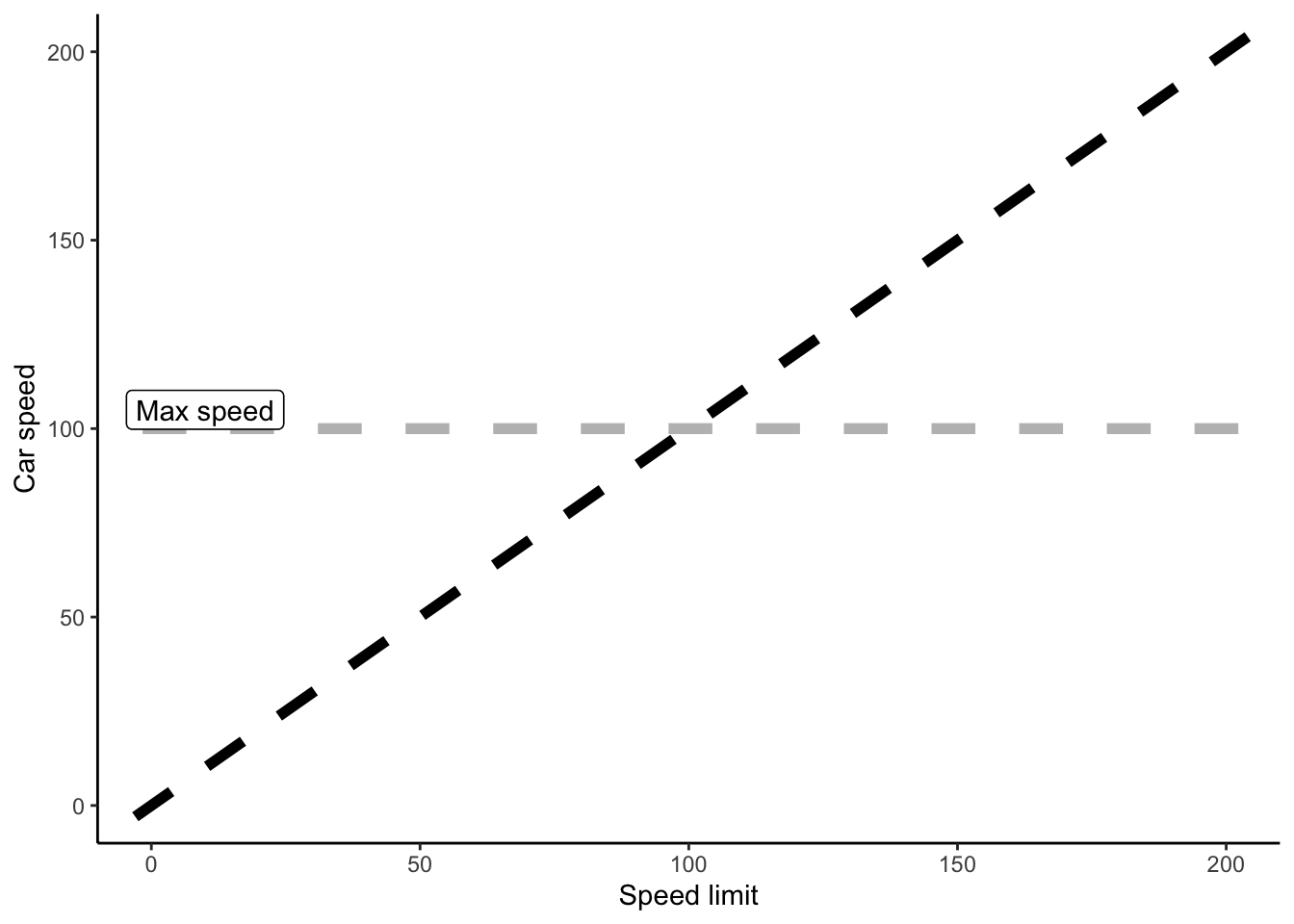

Car speed equals the speed limit, right up to the car’s maximum velocity. Then, it doesn’t matter how high the limit is, the car has to stay at maximum speed.

Not so fast!

Not every car is going to go at the exact manufacturers maximum speed! When (in my imaginary example) manufacturers release a new kind of car, they test a sample of cars to measure their maximum speed. Therefore we know the max speed (with some error) for that brand of car. However, the realized max speed for any specific car in the wild will be lower than this value. This could be caused by a host of unmeasured factors, such as that particular car’s defects, the kind of care it has received, etc

tribble(~ limit, ~ max,
        0, 0,
        200, 200) |> 
  ggplot(aes(x = limit, y = max)) + 
  geom_point(col = "white") + 
  geom_abline(slope = 0, intercept = 100, lty = 2, lwd = 2, col = "grey") + 
  geom_label(aes(x = 25, y = 105, label = "Factory Max speed")) + 
  geom_abline(slope = 0, intercept = 80, lty = 2, lwd = 1, col = "orange") + 
  geom_label(aes(x = 25, y = 85, label = "Actual max speed")) + 
  geom_abline(slope = 1, intercept = 0, lty = 2, lwd = 2) + 
  theme_classic() + 
  labs(x = "Speed limit", y = "Car speed")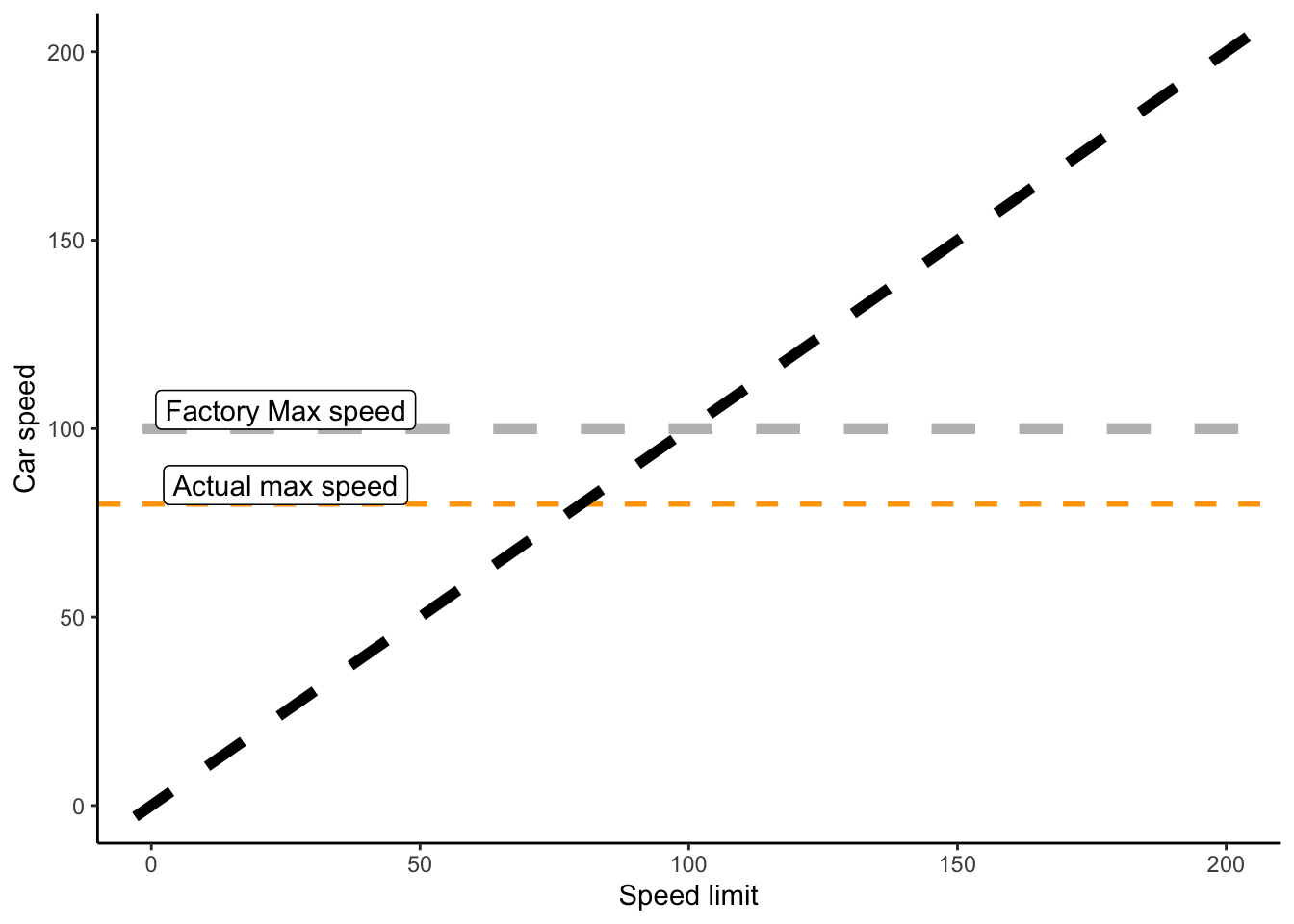

Car speed equals the speed limit, right up to the car’s maximum velocity – decreased a little bit by particularities of this specific car.

Write that in mathematics

for one car, driving on different roads.

  • We label the different roads \(i\)
  • \(\tau\) is the maximum speed of this particular kind of car
  • \(M\) is a bunch of measurements of the car’s max speed (based on factory cars)
  • \(p\) is the proportion of that maximum that our actual car has

\[ \begin{align} Y_i &\sim \text{Normal}(\mu_i, \sigma)\\ M &\sim \text{Normal}(\tau, \sigma_m)\\ \mu_i & = \begin{cases} X_i & \text{if } X_i \leq p\tau \\ p\tau & \text{if } X_i > p\tau \end{cases} \\ \text{logit}(p) &\sim \text{Normal}(2, .5) \\ \tau &\sim \text{Normal}(...) \\ \sigma_m &\sim \text{Exponential}(...) \\ \sigma &\sim \text{Exponential}(...) \end{align} \]

Simple Stan code with prior predictions

breakpoint_B <- cmdstan_model(here::here("posts/2023-07-05-breakpoint/breakpoint_B.stan"))
breakpoint_B
data {
  int n;
  vector[n] x;
  real B;
}
// transformed data {
//   real M = max(x);
// }
parameters {
 real b2;
 real<lower=0> sigma;
}
model {
  b2 ~ normal(1, 1);
  sigma ~ exponential(1);
}
generated quantities {
  vector[n] y;
  for( i in 1:n){
    if (x[i] < B) {
      y[i] = normal_rng(x[i]*b2, sigma);
    } else {
      y[i] = normal_rng(B*b2, sigma);
    }
  }
}
xvar <- runif(42, min = 1, max=55)

breakpoint_B_prior <- breakpoint_B$sample(chains=1,
                                      data = list(x = xvar,
                                                  n = 42,
                                                  B = 25))
Running MCMC with 1 chain...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Iteration:  100 / 2000 [  5%]  (Warmup) 
Chain 1 Iteration:  200 / 2000 [ 10%]  (Warmup) 
Chain 1 Iteration:  300 / 2000 [ 15%]  (Warmup) 
Chain 1 Iteration:  400 / 2000 [ 20%]  (Warmup) 
Chain 1 Iteration:  500 / 2000 [ 25%]  (Warmup) 
Chain 1 Iteration:  600 / 2000 [ 30%]  (Warmup) 
Chain 1 Iteration:  700 / 2000 [ 35%]  (Warmup) 
Chain 1 Iteration:  800 / 2000 [ 40%]  (Warmup) 
Chain 1 Iteration:  900 / 2000 [ 45%]  (Warmup) 
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 1 Iteration: 1100 / 2000 [ 55%]  (Sampling) 
Chain 1 Iteration: 1200 / 2000 [ 60%]  (Sampling) 
Chain 1 Iteration: 1300 / 2000 [ 65%]  (Sampling) 
Chain 1 Iteration: 1400 / 2000 [ 70%]  (Sampling) 
Chain 1 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
Chain 1 Iteration: 1600 / 2000 [ 80%]  (Sampling) 
Chain 1 Iteration: 1700 / 2000 [ 85%]  (Sampling) 
Chain 1 Iteration: 1800 / 2000 [ 90%]  (Sampling) 
Chain 1 Iteration: 1900 / 2000 [ 95%]  (Sampling) 
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 1 finished in 0.0 seconds.
breakpoint_B_prior
 variable  mean median    sd   mad     q5   q95 rhat ess_bulk ess_tail
    lp__  -2.00  -1.69  0.99  0.71  -3.84 -1.05 1.00      423      391
    b2     0.98   0.97  0.91  0.93  -0.56  2.57 1.00      589      609
    sigma  0.99   0.64  1.02  0.66   0.05  3.15 1.00      609      346
    y[1]  24.52  23.87 22.87 23.49 -14.30 64.14 1.00      592      572
    y[2]  24.58  24.27 22.87 23.19 -13.87 63.73 1.00      585      609
    y[3]   3.59   3.42  3.56  3.53  -2.18  9.59 1.00      573      617
    y[4]  24.55  24.04 22.91 23.51 -14.53 63.83 1.00      599      581
    y[5]  24.70  24.28 22.82 22.93 -14.38 64.15 1.00      598      501
    y[6]  15.98  15.66 14.87 14.93  -9.47 42.02 1.00      595      607
    y[7]  24.55  24.02 22.78 23.27 -13.91 63.94 1.00      586      572

 # showing 10 of 45 rows (change via 'max_rows' argument or 'cmdstanr_max_rows' option)

plot it

prior_draws <- breakpoint_B_prior |> 
  tidybayes::gather_draws(y[i], ndraws = 12) |> 
  mutate(x = xvar[i])

prior_draws |> 
  ggplot(aes(x = x, y = .value)) + geom_point() + 
  facet_wrap(~.draw)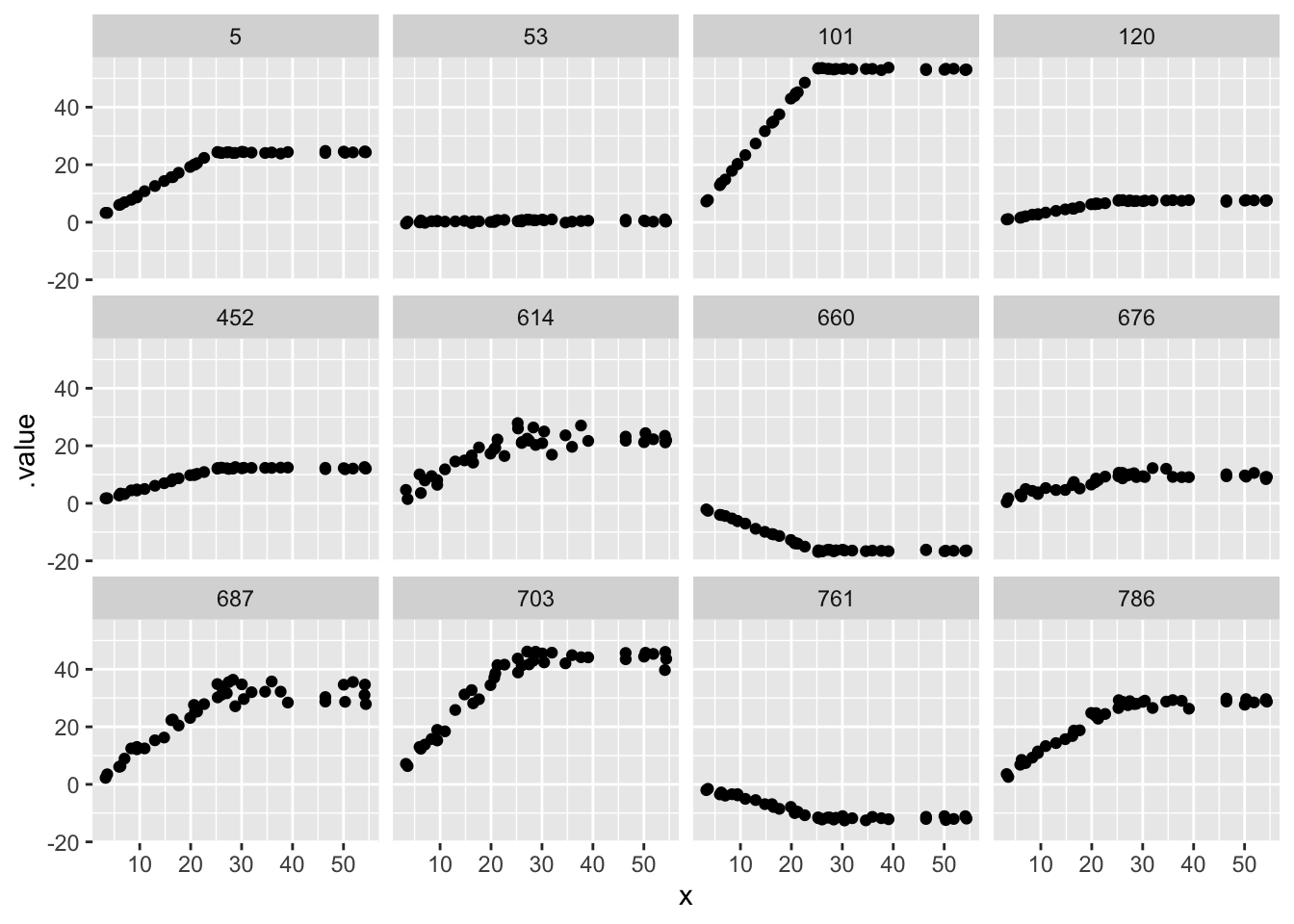

Rewriting this with step()

I learned from PhD student Dominique Caron that breakpoint regression can be written in brms using step(). This is described in this forum discussion and demonstrated in Stan code here. The Stan manual discusses step() among other logical functions

breakpoint_step_prior <- cmdstanr::cmdstan_model(
  here::here("posts/2023-07-05-breakpoint/breakpoint_step_prior.stan"))
breakpoint_step_prior
data {
  int n;
  vector[n] x;
  real B;
}
parameters {
 vector[n] y;
 real<lower=0> sigma;
}
transformed parameters {
  vector[n] x2;
  for (i in 1:n){
    x2[i] = step(B - x[i]);
  }
}
model {
  vector[n] mu;
  mu = B + (x - B) .* x2;
  y ~ normal(mu, sigma);
  sigma ~ exponential(1);
}
set.seed(4812)

xvar <- runif(42, min = 1, max=55)

breakpoint_step_prior_samples <- breakpoint_step_prior$sample(chains=1,
                                      data = list(x = xvar,
                                                  n = 42, B = 33), refresh = 0L)
Running MCMC with 1 chain...

Chain 1 finished in 0.6 seconds.
Warning: 1 of 1 chains had an E-BFMI less than 0.2.
See https://mc-stan.org/misc/warnings for details.
prior_draws <- breakpoint_step_prior_samples |> 
  tidybayes::gather_draws(y[i], ndraws = 12) |> 
  mutate(x = xvar[i])

prior_draws |> 
  ggplot(aes(x = x, y = .value)) + geom_point() + 
  facet_wrap(~.draw)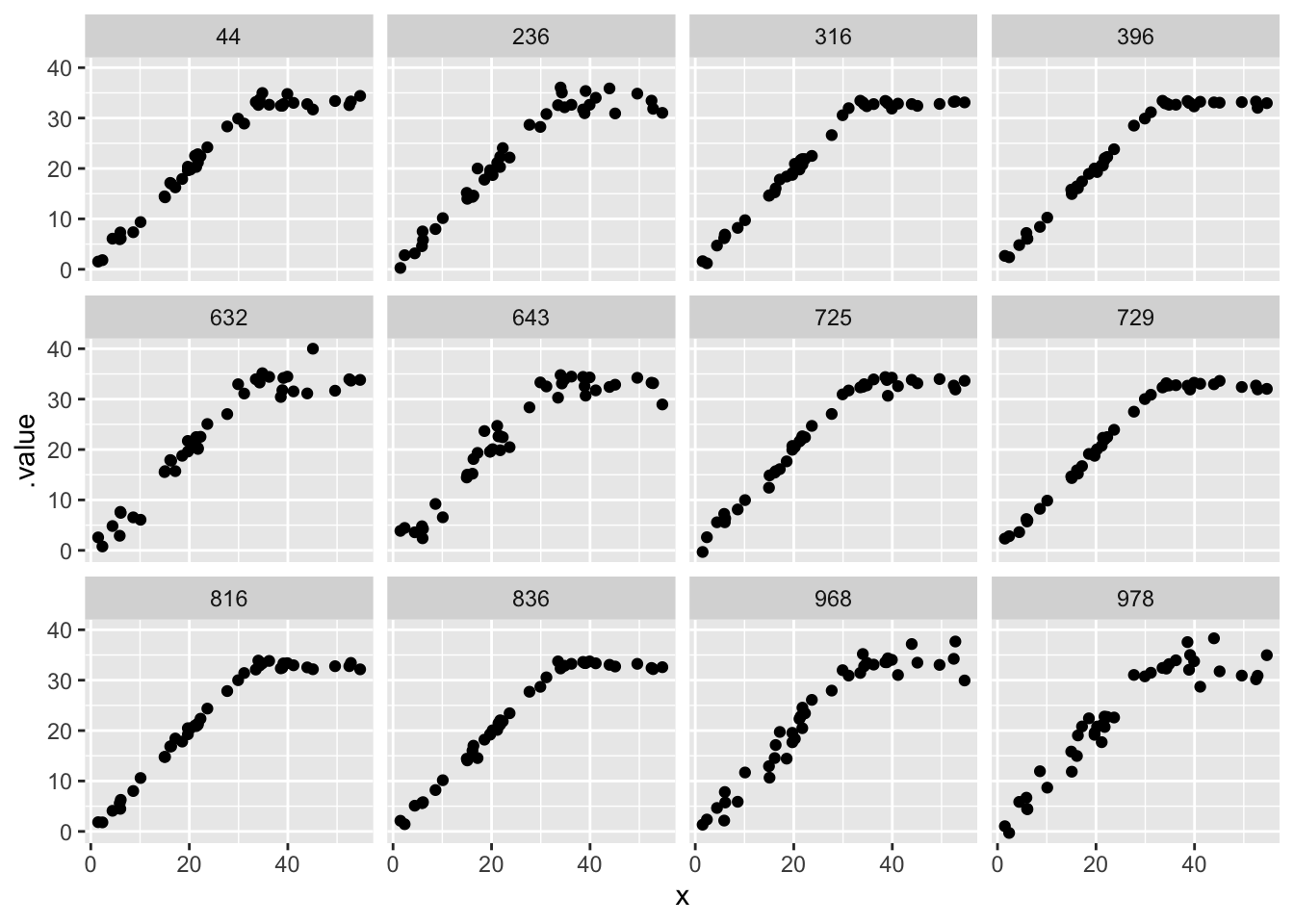

estimating breakpoints with some prior knowledge

We assume here that we have some unmeasured maximum. in my car example, the maximum speed of each kind of car is measured at the factory, by taking a random sample of cars and measuring their max speeds

## take just one 
one_dataset <- prior_draws |> 
  arrange(.draw) |> 
  head(42)

breakpoint_step_meas <- cmdstanr::cmdstan_model(
  here::here("posts/2023-07-05-breakpoint/breakpoint_step_meas.stan"))

breakpoint_step_meas
data {
  int n;
  vector[n] speed_limit;
  vector[n] obs_speed;
  real max_avg;
  real max_sd;
}
parameters {
  real max_speed;
  real<lower=0> sigma;
}
transformed parameters {
  vector[n] V2;
  for (i in 1:n){
    V2[i] = step(max_speed - speed_limit[i]);
  }
}
model {
  vector[n] mu;
  mu = max_speed + (speed_limit - max_speed) .* V2;
  max_speed ~ normal(max_avg, max_sd);
  obs_speed ~ normal(mu, sigma);
  sigma ~ exponential(1);
}
breakpoint_step_meas$sample(data = list(n  = 42, speed_limit = one_dataset$x, 
                                        obs_speed = one_dataset$.value,
                                        max_avg = 30,
                                        max_sd = 5), refresh = 0L)
Running MCMC with 4 sequential chains...

Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 finished in 0.1 seconds.
Chain 4 finished in 0.1 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.7 seconds.
Warning: NAs introduced by coercion

Warning: NAs introduced by coercion
  variable   mean median   sd  mad     q5    q95 rhat ess_bulk ess_tail
 lp__      -18.53 -18.23 0.99 0.71 -20.57 -17.57 1.00     1745     1892
 max_speed  33.17  33.17 0.23 0.23  32.79  33.54 1.00     2427     2370
 sigma       0.93   0.91 0.11 0.10   0.77   1.11 1.00     3100     2272
 V2[1]       1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA
 V2[2]       1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA
 V2[3]       1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA
 V2[4]       0.00   0.00 0.00 0.00   0.00   0.00   NA       NA       NA
 V2[5]       1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA
 V2[6]       0.00   0.00 0.00 0.00   0.00   0.00   NA       NA       NA
 V2[7]       1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA

 # showing 10 of 45 rows (change via 'max_rows' argument or 'cmdstanr_max_rows' option)

Objects on the road are slower than they appear

the factory-measured speed is probably a lot higher than the top speed of the average car on the road. lots of factors intervene: the particular car’s defects, its maitenance history, the fuel used, the driver’s skill.

All of these factors will only DECREASE, and never increase, a car’s speed relative to the maximum possible.

breakpoint_step_p <- cmdstanr::cmdstan_model(
  here::here("posts/2023-07-05-breakpoint/breakpoint_step_p.stan"))
breakpoint_step_p
data {
  int n;
  vector[n] speed_limit;
  vector[n] obs_speed;
  real max_avg;
  real max_sd;
}
parameters {
  real factory_speed;
  real<lower=0> sigma;
  real alpha;
}
transformed parameters {
  real max_speed;
  max_speed = factory_speed * inv_logit(alpha);
  vector[n] V2;
  for (i in 1:n){
    // step() is 0 if speed limit is over the maximum, 0 otherwise
    // in other words, it gives the slope
    V2[i] = step(max_speed - speed_limit[i]);
  }
}
model {
  vector[n] mu;
  mu = max_speed + (speed_limit - max_speed) .* V2;
  factory_speed ~ normal(max_avg, max_sd);
  obs_speed ~ normal(mu, sigma);
  alpha ~ normal(3, 2);
  sigma ~ exponential(1);
}
breakpoint_step_p$sample(data = list(n  = 42, 
                                     speed_limit = one_dataset$x, 
                                     obs_speed = one_dataset$.value,
                                     max_avg = 30,
                                     max_sd = 5), refresh = 0L)
Running MCMC with 4 sequential chains...

Chain 1 finished in 0.2 seconds.
Chain 2 finished in 0.2 seconds.
Chain 3 finished in 0.2 seconds.
Chain 4 finished in 0.2 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.2 seconds.
Total execution time: 1.1 seconds.
Warning: 80 of 4000 (2.0%) transitions ended with a divergence.
See https://mc-stan.org/misc/warnings for details.
Warning: NAs introduced by coercion

Warning: NAs introduced by coercion
      variable   mean median   sd  mad     q5    q95 rhat ess_bulk ess_tail
 lp__          -19.12 -18.82 1.21 0.95 -21.47 -17.84 1.01      985     1660
 factory_speed  33.84  33.68 0.66 0.57  33.03  35.09 1.01      232      109
 sigma           0.93   0.92 0.11 0.10   0.77   1.11 1.01      539      997
 alpha           4.45   4.24 1.25 1.28   2.82   6.74 1.01      237      135
 max_speed      33.16  33.17 0.24 0.23  32.76  33.55 1.00     2243      727
 V2[1]           1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA
 V2[2]           1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA
 V2[3]           1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA
 V2[4]           0.00   0.00 0.00 0.00   0.00   0.00   NA       NA       NA
 V2[5]           1.00   1.00 0.00 0.00   1.00   1.00   NA       NA       NA

 # showing 10 of 47 rows (change via 'max_rows' argument or 'cmdstanr_max_rows' option)

first thing that doesn’t work well (admittedly, there is nothing in these simulated data to support this)

suggestion that the probability prior is very important

perhaps if the same kind of car travelled on different highways in several different countries? in all countries the car would have the same theoretical maximum, but the difference in country-level factors mean that the proportion \(p\) below that max, where the average car has its top speed, is going to vary.

what other uncertainty is there to include? uncertainty in the speed limit perhaps?

switch for gamma errors

Before advancing model building much farther, I want to correct the error distribution. Speeds might be variable, but they can never be negative!

breakpoint_step_gamma_prior <- cmdstanr::cmdstan_model(
  here::here("posts/2023-07-05-breakpoint/breakpoint_step_gamma_prior.stan"))
breakpoint_step_gamma_prior
data {
  int n;
  vector[n] x;
  real B;
}
parameters {
 vector<lower=0>[n] y;
 real<lower=0> sigma;
}
transformed parameters {
  vector[n] x2;
  for (i in 1:n){
    x2[i] = step(B - x[i]);
  }
}
model {
  vector[n] mu;
  mu = B + (x - B) .* x2;
  vector[n] beta = mu/square(sigma);
  y ~ gamma(mu .* beta, beta);
  sigma ~ exponential(1);
}
set.seed(4812)

xvar <- runif(42, min = 1, max = 55)

breakpoint_step_gamma_prior_samples <- breakpoint_step_gamma_prior$sample(
  chains=1,
  data = list(x = xvar,
              n = 42, B = 33), refresh = 1000L)
Running MCMC with 1 chain...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Random variable[1] is inf, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Random variable[1] is inf, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Random variable[4] is inf, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Shape parameter[1] is 0, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Shape parameter[1] is 0, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Shape parameter[1] is 0, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Shape parameter[1] is 0, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Shape parameter[1] is inf, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Shape parameter[1] is inf, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
Chain 1 Exception: gamma_lpdf: Shape parameter[1] is inf, but must be positive finite! (in '/var/folders/x7/l08zn2396g797m5ws54np_6w0000gp/T/Rtmp5fMbyc/model-5cb742e1f51c.stan', line 20, column 2 to column 30)
Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
Chain 1 
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 1 finished in 0.5 seconds.
Warning: 1 of 1 chains had an E-BFMI less than 0.2.
See https://mc-stan.org/misc/warnings for details.
prior_draws <- breakpoint_step_gamma_prior_samples |> 
  tidybayes::gather_draws(y[i], ndraws = 12) |> 
  mutate(x = xvar[i])

prior_draws |> 
  ggplot(aes(x = x, y = .value)) + 
  geom_point() + 
  facet_wrap(~.draw)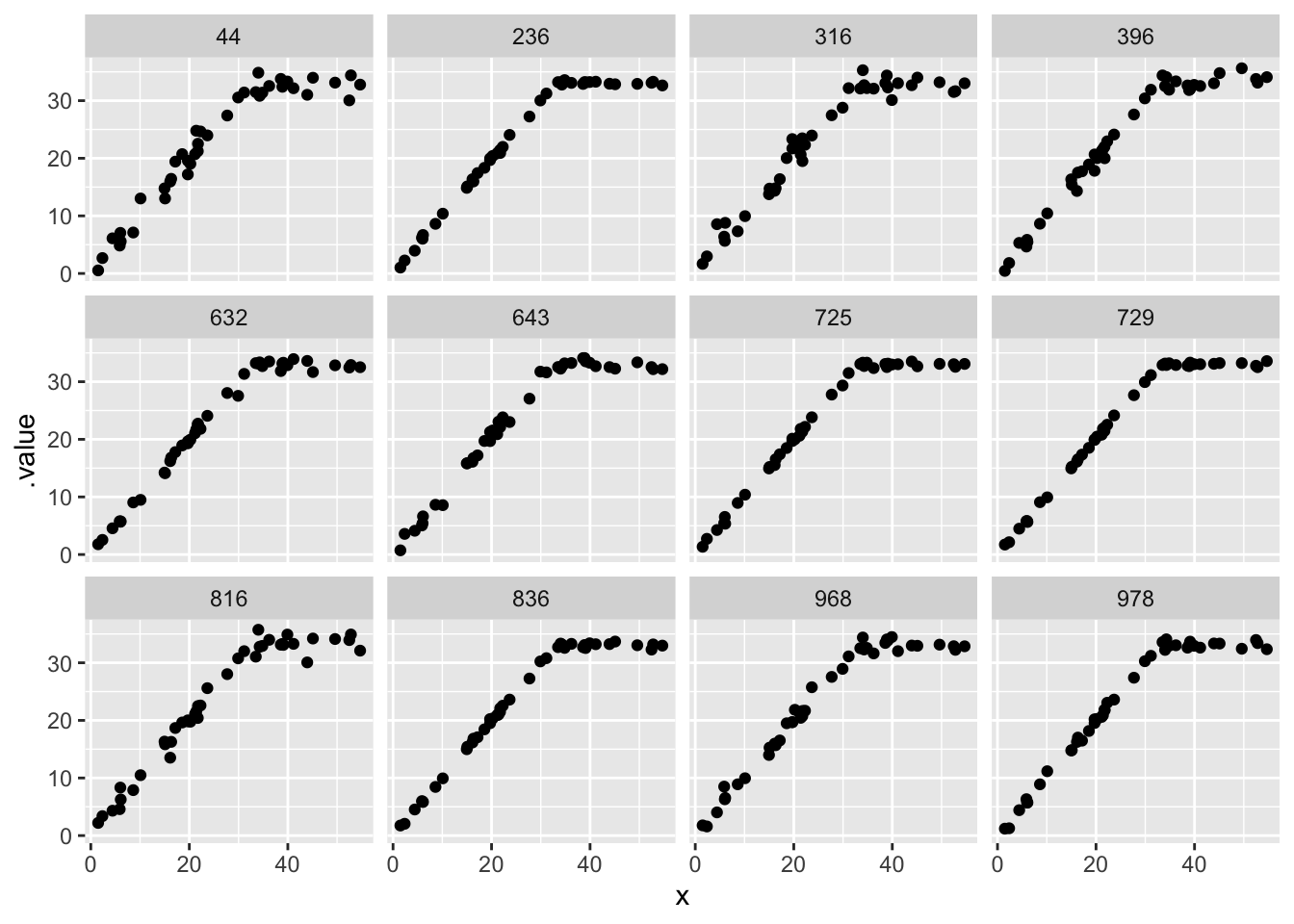

Footnotes

  1. see Leibig’s Law of the Minimum, and also Dune↩︎